感知机
Table of Contents
二类分类的线性分类模型 输入：实例的特征向量 输出：实例的类别
感知机模型
f(x) = sign(w*x + b) if(x >= 0) sign(x) = 1; else sign(x) = -1;
感知机学习策略
数据集的线性可分性
感知机学习策略
确定学习策略，即定义损失函数并使损失函数最小化
感知机采用损失函数输入特征：误分类点到超平面的距离
感知机损失函数定义:
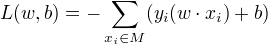其中，M是误分类点的集合。
给定数据集T,损失函数是w,b的连续可导函数
感知机学习算法
求解损失函数的最优化问题的方法。 梯度下降法， 原始形式、对偶形式
感知机学习算法的原始形式
误分类驱动 梯度下降法
一次随机选取一个误分类点使其梯度下降
随机选取一个误分类点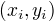 
, 对w,b进行更新：
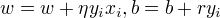采用不同的初值或者选取不同的分类点，解可以不同。
算法的收敛性
当训练数据集线性可分时，感知机学习算法原始形式是迭代收敛的，当不可分时，迭代不收敛