提升方法
Table of Contents
在分类中，boosting 通过改变训练样本的权重，学习多个分类器，并将这些分类器进行线性组合，提高分类的性能。
提升方法AdaBoost算法
提升方法的基本思路
PAC(probably approximately correct)概率近似正确 强可学习和弱可学习等价 将弱可学习算法提升为强可学习算法, adaboost 提升方法从弱学习算法出发，反复学习，得到一系列弱分类器（基本分类器），然后组合弱分类器，构成一个强分类器。大多数的提升方法都是改变训练数据的概率分布，针对不同的数据分布学得不同的弱学类器。
如何改变训练数据的权值和概率分布 Adaboost:提高那些被前一轮弱分类器错误分类样本的权值，而降低那些被正确分类样本的权值。
如何将弱分类器组合成一个强分类器 Adaboost:加权多数表决，加大分类误差率小的弱分类器的权值，减小分类误差率大的权值。
Adaboost算法
Adaboost的例子
Adaboost算法的训练误差分析
Adaboost的训练误差是以指数速率下降的。具有适应性，能适应弱分类器各自的训练误差率。
Adaboost算法的解释
另一种解释，模型为加法模型，损失函数为指数函数、学习算法为前向分布算法的二类分类学习方法。
前向分布算法
前向分布算法与Adaboost
提升树
以分类树或者回归树为基本分类器的提升方法。
提升树模型
可以表示为决策树的加法模型：
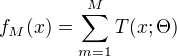其中，T表示决策树，
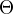为决策树参数； M为树的个数。
提升树算法
采用前向分步算法。
首先确定初始提升树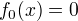 
,第m步的模型是：
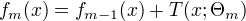通过经验风险极小化确定下一棵决策树的参数 
.
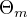树的线性组合能很好地拟合训练数据，提升树是一个高功能算法。
不同的提升树算法，其区别是损失函数不同。
回归问题：使用平方误差损失函数
分类问题：使用指数损失函数
一般决策问题：一般损失函数
二类分类问题，将adaboost中的基本分类器限定为二类分类器，提升树是Adaboost的特殊情况。 回归问题的提升树只需简单地拟合当前模型的残差。
回归问题的提升树算法：
输入：训练数据集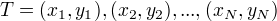 
输出：提升树 
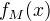(1)初始化 
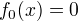(2)对m=1,2,…,M
(a)计算残差
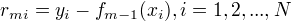(b)拟合残差$rmi$学习一个回归树，得到T
(c)更新fm(x) = fm-1(x) + T
(3)得到回归问题提升树
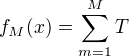
梯度提升
对一般损失函数，提升树的优化并不容易。梯度提升，利用最速下降法的近似方法，利用损失函数的负梯度在当前模型的值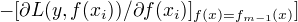 
作为回归问题提升树算法中残差的近似值，拟合一个回归树。
算法步骤： (1)初始化：估计使损失函数极小化的常数值，是只有根结点的树。 (2a)计算损失函数的负梯度在当前模型的值，将它作为残差的估计。 (2b)估计回归树叶结点区域，以拟合残差的近似值。 (2c)利用线性搜索估计叶节点区域的值，使损失函数极小化。 (2d)更新回归树 (3)得到最终模型