支持向量机
Table of Contents
在特征空间间隔最大大的线性分类器。 核技巧,非线性分类器 学习策略:间隔最大化m 学习算法是求解凸二次规划的最优化算法
模型:线性可分支持向量机、线性支持向量机、非线性支持向量机(由简到繁) 训练数据线性可分 硬间隔最大化 线性可分支持向量机 训练数据近似可分 软间隔最大化 线性支持向量机 训练数据线性不可分 核技巧和软间隔最大化 非线性支持向量机
输入空间是欧式空间或者离散集合、特征空间是希尔伯特空间时,核函数:将输入从输入空间映射到特征空间得到特征向量之间的内积。 核方法是比支持向量机更为一般的机器学习方法。
线性可分支持向量机和硬间隔最大化
线性可分支持向量机
利用间隔最大化求最优分离超平面,解唯一。
函数间隔和几何间隔
函数间隔
样本点 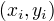 的函数间隔:
的函数间隔:
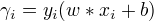 关于训练集的函数间隔:
关于训练集的函数间隔:
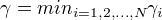 对w进行约束,||w|| = 1,函数间隔变成几何间隔
对w进行约束,||w|| = 1,函数间隔变成几何间隔
间隔最大化
最大间隔分离超平面
线性可分支持向量机学习的最优化问题:
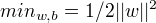
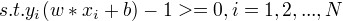 最大间隔分离超平面的存在具有唯一性
最大间隔分离超平面的存在具有唯一性
支持向量和间隔边界
训练样本点与分离超平面距离最近的实例为支持向量
学习的对偶算法
优点:对偶问题往往更容易求解、自然引入核函数,推广到非线性分类
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
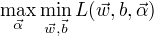 为了得到对偶问题的解,需要先求
为了得到对偶问题的解,需要先求 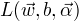 对
对 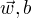 的极小化,接着求对
的极小化,接着求对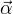 的极大化。
与之等价的对偶最优化问题:
的极大化。
与之等价的对偶最优化问题:
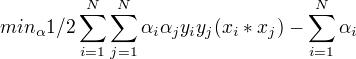
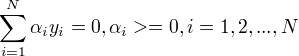 分类决策函数只依赖于输入x和训练样本输入的内积
分类决策函数只依赖于输入x和训练样本输入的内积
对于给定的线性可分训练集,通过对偶问题求得w,b, 得到分离超平面和分类决策函数。这种方法是线性可分支持向量机的基本学习算法。
w,b只依赖于训练样本中对应于 $αi > 0 $ 的样本点,将这样的点称为支持向量。
线性支持向量机与软间隔最大化
线性支持向量机
引入松弛变量 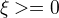 ,使函数间隔加上松弛变量大于等于0,约束条件变为:
,使函数间隔加上松弛变量大于等于0,约束条件变为:
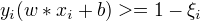 目标函数变为:
目标函数变为:
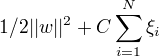 C > 0称为惩罚参数
使
C > 0称为惩罚参数
使 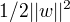 尽量小即间隔尽量大,使误分类的额个数尽量小
线性不可分的线性支持向量机学习的原始问题:
尽量小即间隔尽量大,使误分类的额个数尽量小
线性不可分的线性支持向量机学习的原始问题:
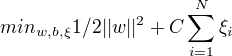
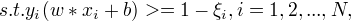
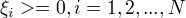 可以证明w的解是唯一的,b的解不唯一,存在一个区间
可以证明w的解是唯一的,b的解不唯一,存在一个区间
学习的对偶算法
原始问题对应的对偶问题不变,满足的条件发生改变 $ 0<= αi <= C, i=1,2,…N$
支持向量
软间隔的支持向量或者在间隔的边界上,或者在间隔边界与分离超平面之间,或者在分离超平面误分类一侧。
合页损失函数
线性支持向量机学习,模型:分离超平面及决策函数,学习策略:软间隔最大化,学习算法:凸二次规划
另一种解释,最小化如下目标函数:
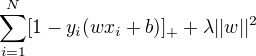 目标函数的第一项称为经验损失,第一项称为合页损失函数,第二项是正则化项。
目标函数的第一项称为经验损失,第一项称为合页损失函数,第二项是正则化项。
非线性支持向量机和核函数
核技巧
核技巧通过一个非线性变换将输入空间对应与一个特征空间。分类任务在特征空间求解线性支持向量机。
存在输入空间到特征空间的映射
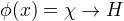 使得对所有的
使得对所有的 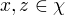 ,函数K(x,z)满足条件
,函数K(x,z)满足条件
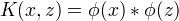 则称K(x,z)为核函数(任意两个输入变量在高维映射中的内积),
则称K(x,z)为核函数(任意两个输入变量在高维映射中的内积), 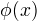 为映射函数。
核技巧:只定义核函数,而不显示地定义映射函数。直接计算核函数容易,而通过映射函数计算复杂。
对于给定的核函数,特征空间和映射函数大的取法不唯一。
为映射函数。
核技巧:只定义核函数,而不显示地定义映射函数。直接计算核函数容易,而通过映射函数计算复杂。
对于给定的核函数,特征空间和映射函数大的取法不唯一。
核技巧在支持向量机中的应用
在对偶的目标函数中的内积 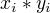 可以用核函数
可以用核函数 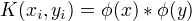 来代替,同时分类决策函数中的内积也可以用核函数来代替。
来代替,同时分类决策函数中的内积也可以用核函数来代替。
正定核
K(x,z)为对称函数,则K(x,z)为正定核函数的充要条件是对任意的 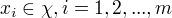 K(x,z)对应的Gram矩阵:
K(x,z)对应的Gram矩阵:
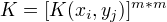 是半正定矩阵。
检验是否是正定核函数并不容易。
是半正定矩阵。
检验是否是正定核函数并不容易。
常用核函数
多项式核函、高斯核函数、字符串核函数 字符串核函数:两个字符串相同的子串越多,他们就越相似,字符串核函数的值就越大。可以由动态规划快速计算。
非线性支持向量分类机
将线性支持向量机扩展到非线性支持向量机,只需将线性支持向量机对偶形式中的内积换成核函数。
非线性支持向量机学习算法
(1)选取适当的核函数K(x,z)和适当的参数C,构造并求解最优化问题
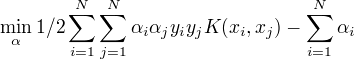
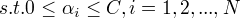
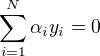 求得最优解
求得最优解 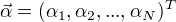 选取
选取 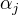 求
求
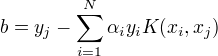 构造决策函数
构造决策函数
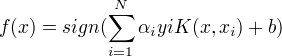
序列最小最优化算法
SMO算法:若所有变量的解都满足KKT条件,则解就得到了;否则,选择两个变量,固定其他变量,构建二次规划问题并求解,将原问题不断分解为子问题并对子问题求解,进而求解原问题。 包含:求解两个变量二次规划的解析方法、选择变量的启发式方法
两个变量二次规划的求解方法
变量选择的方法
第1个变量的选择 外层循环选取违背KKT条件最严重的点,首先遍历在间隔边界上的支持向量的点,检验是否满足条件,若都满足条件,则遍历整个训练集,检验是否满足条件。 第2个变量的选择 选择的标准,使第二个变量有足够大的变化
